Comparison of seven wind gust parameterizations over the European part of Russia
Maria Kurbatova
Konstantin Rubinstein
Inna Gubenko
Grigory Kurbatov
Wind gusts are extreme events which can cause severe damage. Gusts can reach significant values even during medium winds. However, numerical atmospheric models are designed to reproduce average wind speed, not gusts. There are several approaches to estimating wind gusts. Seven different methods are applied to WRF-ARW model output. Results are compared to high-frequency wind speed measurements using ultrasonic anemometers and temperature profiler measurement at the same point in Moscow. Data gathered from synoptic station network over the European part of Russia were also included in the analysis to increase the statistics. None of the wind gust estimation methods shows best results at every skill score. The proposed hybrid method shows good balance between the probability of detection and the false alarm ratio estimates.
Even when average wind speed is low gusts can reach significant values. Gusts carry a high amount of wind energy and can cause severe damage and affect transport functioning. The greatest damage from storms is usually caused by strong wind gusts leading to constructions collapse and falling trees. For example, due to the storm over Moscow in May 2017, 16 people died, and according to insurance companies, the economic loss exceeded 25 million roubles (≈350 000 EUR). Major damage appeared because of torn-off roofs, weak constructions, breakage of power lines, trees falling on cars – the reason for all of this was the strong wind. Early forecast of strong wind gusts can help to organize preventive actions (strengthening structures, warning people, etc.) to reduce damage, so realistically forecasting wind gusts is a very important task of numerical meteorology. However, there is a variety of methods for wind gust estimation. There is a need to know the applicability of the method used in a particular case. In this study we analyse different aspects of wind gust forecast approaches.
There are two ways to use numerical model output: to perform statistical postprocessing or to create a physical model of wind gust formation. The undoubted advantage of the second approach is that these methods help to better understand the nature and mechanisms of the formation of this natural phenomenon. Let us analyse this group of methods in more detail.
Dynamical wind gust estimation methods can be divided into two groups. Methods in the first group are based on the fact that wind gusts are related to atmospheric turbulence and therefore can be estimated on the basis of turbulent characteristics determined within the parameterization of the atmospheric boundary layer. Turbulent kinetic energy (TKE) represents a deviation of the instantaneous wind from the mean, so we can consider TKE as wind speed dispersion. From the assumption that the wind speed distribution is normal, the following formula can be proposed (this method is further referred to as TKE):
where “wge” is the wind gust estimate, U is average wind speed, σ is the standard deviation of wind speed, and q is TKE. If there is no TKE in the model output, we can use the relation between TKE and friction velocity to estimate the variance (Born et al., 2012). If we assume that the TKE in the model represents the maximum deviation of instant wind from the mean, we can get the following estimate (Born et al., 2012) (this method is further referred to as TKE-2):
Another TKE-based parameterization was developed by Schreur and Geertsema (2008) (this method is further referred to as Schreur):
Based on the observation data fit:
where t=3 s is gust duration and z=10 m is height above ground.
Methods in the second group are based on an assumption that gusts are the result of air particles deflection from higher levels and carry speed from those levels. Bradbury et al. (1994) proposed to use the wind speed from the atmospheric boundary layer height (this method is further referred to as PBLH).
In the case of deep convection, vertical motion as well as precipitation should be taken into account (Nakamura et al., 1996) (this method is further referred to as Nakamura):
where H is boundary layer height, and qris rain mixing ratio, Nakamura et al. (1996) suggests α=0.25 and β=0.85.
Brasseur (2001) suggests taking into account the energy of particles that can reach the surface (this method is further referred to as Brasseur):
for the levels zp satisfying Eq. (8):
where θv is the virtual potential temperature.
The methods using TKE are not applicable to the prediction of gusts associated with strong convection. However, they work well in cases with the turbulence of mechanical origin. Our preliminary study showed the first TKE method to give good results. Otherwise, particle deflection methods are usually considered in cases of convection. The Brasseur method looks to be the most physically developed. To combine advantages of both groups of methods we propose a hybrid method:
where zp satisfies Eq. (8). We use the Richardson number Ri to separate the types of the instability of the atmospheric boundary layer.
3.1 Measurement data and numerical model
Unfortunately, the measurements that allow the dynamics of wind gust formation to be studied are rather sparse. In this paper, we use data from high-frequency wind speed measurements conducted at the Physics Department of Moscow State University in Moscow. The measurements are carried out at a frequency of 50 Hz with ultrasonic anemometers USA-1 (Metek). At the same point, the temperature profiles up to 600 m height are measured using a microwave temperature profiler MTP-5.
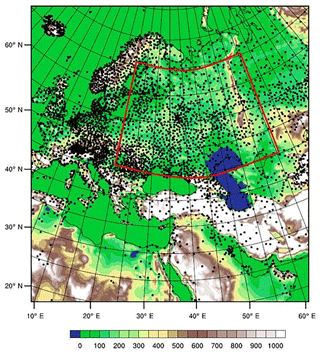
Wind gusts are observed by synoptic stations network but data contain many omissions (only 25 % reports contain gust information) and have 3 h time resolution. In addition, gusts associated with the squall lines may have a small spatial extent, so they are not captured by data. However, the network provides the biggest data set over the European part of Russia: 2189 stations were used in this work (see Fig. 1).
Wind gust estimation methods are realized using WRF-ARW version 3.7.1 (Skamarock and Klemp, 2008) model output. It has good estimations of the forecast of meteorological values in the atmospheric boundary layer (Smirnova et al., 2011). The model domain (Fig. 1) covers the European part of Russia with a spatial resolution of 18 km. The initial and boundary conditions are the NCEP analysis (Kanamitsu et al., 1991) with a spatial resolution of 0.5∘. The model configuration was chosen on the basis of studies in which an accurate description of the wind speed is important (Coniglio et al., 2013; Giannakopoulou and Nhili, 2014). The model parameterizations include microphysics (Thompson et al., 2004), radiation – RRTMG (Iacono et al., 2008), soil – NOAH (Tewari et al., 2004), Bates–Miller convection (Janjić, 1994), and boundary layer – MYNN (Nakanishi and Niino, 2006).
3.2 Method of evaluation
Seven methods described in Sect. 2 were applied to WRF model output (3 h time step) at each grid point. To obtain mean wind speed values from the four nearest model grid points are bilinearly interpolated to the measurement point. To obtain the wind gust estimation, the maximum value from the four nearest grid points is taken. Gust observation is at a maximum over at 10 min period from a 3 s average at the point with high-frequency measurements. Temperature profile measurements are averaged for the same 10 min intervals.
For comparison with the data from the synoptic network, the area shown on Fig. 1 was divided into 1∘ × 1∘ cells in latitude and longitude. The value in the cell is maximum gust from all stations and from all computational model points in this cell. If there were no observations in the cell, it is not taken into account. This sort of averaging was done to reduce phase errors. It can lead to overestimating gusts, especially in highly variable terrain. However, the analysed area is mostly relatively flat. The wind gust exceeding of the preset threshold 15 m s−1 is taken as an actual event. The probability of detection, false alarm ratio, Pierce's skill score (PSS), and equitable threat score (ETS) were calculated based on the contingency table compilation.
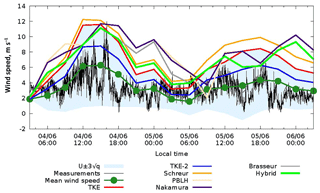
Figure 2Time series for 4–6 June 2016 of measured wind speed with 3 s averaging and one forecast starting at 03:00 LT on 4 June of wind speed and gusts by seven methods described in Sect. 2.
Figure 2 shows the example of high-frequency wind speed measurements and the forecast of wind speed and gusts calculated by seven parameterizations. Mean wind speed is quite well reproduced by the model. Figure 2 shows an interval too; thus in the TKE method is taken as the standard deviation of wind speed. Analysis of 1-year data (0–48 h lead-time forecasts starting every 24 h) showed that 74 % of all measurements fit this interval. Most deviations from observations are due to time-phase errors of mean wind speed. Though most methods capture the strongest gust in the shown period, they overestimate them most of the time.
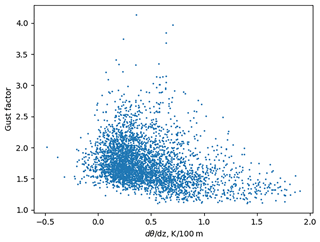
Figure 3 presents the measured gust factor and the potential temperature gradients in the lower 100 m layer. It does not show a direct connection between them. However gust factor spreading increases if the potential temperature gradient decreases.
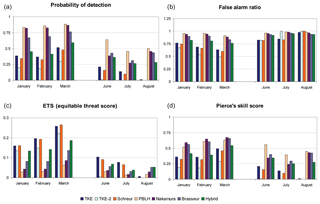
Figure 4 shows skill scores of 24 h forecasts of wind gusts exceeding 15 m s−1 for the three winter and three summer months in 2016. Methods using the principle of deviation from higher levels show a higher probability of detection of wind gusts but also a greater number of false alarms. ETS and PSS are low for all methods, especially for summer. Lower performance in summer can be due to the difficulty of describing convective winds. Convective events might not be captured by the model due to its resolution. ETS is slightly better for TKE using methods since they have a lower false alarm ratio. PSS is slightly greater for particle deflection methods since they have higher probability of detection. Despite the fact that the hybrid method does not show the best estimate, it has a greater probability of detection than TKE methods and a lower false alarm ratio then particle deflection methods. It can be seen that none of the existing methods provide high performance in every skill score, so there is a need for further investigation of gusts.
Seven wind gust estimation methods are applied to the WRF-ARW model output. A new hybrid method was proposed. It shows a good balance between the probability of detection and the false alarm ratio estimates. The conducted research shows the necessity of further studying the mechanisms of formation and methods for forecasting of wind gusts.
Data used in this study are not publicly available. Please contact authors for further information.
MK performed numerical experiments, statistical estimations, analysis of the results, and wrote the paper. IG carried out numerical experiments and analysis of the results. KR helped in the formulation of the task, analysis of the results, and writing of the paper. GK performed and analysed high-frequency observations.
The authors declare that they have no conflict of interest.
This article is part of the special issue “17th EMS Annual Meeting: European Conference for Applied Meteorology and Climatology 2017”. It is a result of the EMS Annual Meeting: European Conference for Applied Meteorology and Climatology 2017, Dublin, Ireland, 4–8 September 2017.
This work is partly supported by RFBR according to the research projects 16-05-00822,
16-05-00704, 18-05-00044. It was also supported by EMS through YSTA.
Edited by: Sabrina Wahl
Reviewed by: Ken Mylne and one anonymous referee
Born, K., Ludwig, P., and Pinto, J. G.: Wind gust estimation for Mid-European winter storms: towards a probabilistic view, Tellus A, 64, 17471, https://doi.org/10.3402/tellusa.v64i0.17471, 2012. a, b
Bradbury, W., Deaves, D., Hunt, J., Kershaw, R., Nakamura, K., Hardman, M., and Bearman, P.: The importance of convective gusts, Meteorol. Appl., 1, 365–378, 1994. a
Brasseur, O.: Development and application of a physical approach to estimating wind gusts, Mon.Weather Rev., 129, 5–25, 2001. a
Coniglio, M. C., Correia Jr., J., Marsh, P. T., and Kong, F.: Verification of convection-allowing WRF model forecasts of the planetary boundary layer using sounding observations, Weather Forecast., 28, 842–862, 2013. a
Giannakopoulou, E.-M. and Nhili, R.: WRF model methodology for offshore wind energy applications, Adv. Meteorol., 2014, 319819, https://doi.org/10.1155/2014/319819, 2014. a
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D.: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models, J. Geophys. Res.-Atmos., 113, D13103, https://doi.org/10.1029/2008JD009944, 2008. a
Janjić, Z. I.: The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes, Mon. Weather Rev., 122, 927–945, 1994. a
Kanamitsu, I., Alpert, J., Campana, K., Caplan, P., Deaven, D., Iredell, M., Katz, B., Pan, H.-L., Sela, J., and White, G.: Recent changes implemented into the global forecast system at NMC, Weather Forecast., 6, 425–435, 1991. a
Nakamura, K., Kershaw, R., and Gait, N.: Prediction of near-surface gusts generated by deep convection, Meteorol. Appl., 3, 157–167, 1996. a, b
Nakanishi, M. and Niino, H.: An improved Mellor–Yamada level-3 model: Its numerical stability and application to a regional prediction of advection fog, Bound.-Lay. Meteorol., 119, 397–407, 2006. a
Schreur, B. W. and Geertsema, G.: Theory for a TKE based parameterization of wind gusts, in: HIRLAM newsletter, Citeseer, 54, 177–188, 2008. a
Skamarock, W. and Klemp, J.: A Time-Split Non-Hydrostatic Atmospheric Model, J. Comput. Phys., 227, 3645–3485, 2008. a
Smirnova, M., Rubinshtein, K., and Yushkov, V.: Evaluation of atmospheric boundary layer characteristics simulated by the regional model, Russ. Meteorol. Hydrol., 36, 777–785, 2011. a
Tewari, M., Chen, F., Wang, W., Dudhia, J., LeMone, M., Mitchell, K., Ek, M., Gayno, G., Wegiel, J., and Cuenca, R.: Implementation and verification of the unified NOAH land surface model in the WRF model, in: vol. 1115, 20th conference on weather analysis and forecasting/16th conference on numerical weather prediction, 11–15 January 2004, Seattle, 2004. a
Thompson, G., Rasmussen, R. M., and Manning, K.: Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part I: Description and sensitivity analysis, Mon. Weather Rev., 132, 519–542, 2004. a