Dynamic model of photovoltaic module temperature as a function of atmospheric conditions

The temperature of photovoltaic modules is modelled as a dynamic function of ambient temperature, shortwave and longwave irradiance and wind speed, in order to allow for a more accurate characterisation of their efficiency. A simple dynamic thermal model is developed by extending an existing parametric steady-state model using an exponential smoothing kernel to include the effect of the heat capacity of the system. The four parameters of the model are fitted to measured data from three photovoltaic systems in the Allgäu region in Germany using non-linear optimisation. The dynamic model reduces the root-mean-square error between measured and modelled module temperature to 1.58 K on average, compared to 3.03 K for the steady-state model, whereas the maximum instantaneous error is reduced from 20.02 to 6.58 K.

1 Introduction

Photovoltaic (PV) systems have become an integral part of electricity grids worldwide, in particular due to a dramatic reduction in costs as well as the drive to mitigate anthropogenic climate change using renewable energy sources. Accurate modelling of PV power production in the field is important for several reasons: (i) forecasts of solar PV power production are becoming indispensable for grid operators, (ii) improvements in performance and efficiency need to be properly characterised under different environmental conditions and (iii) in the meteorological context, it is conceivable that PV power data could be used to gain more information about atmospheric optical properties. Since PV module efficiency is dependent on temperature, an incorrect thermal model will in the end lead to errors in the overall power model, especially in the case of rapidly fluctuating atmospheric conditions such as inhomogeneous cloudiness. Under high irradiance variability, a simplified steady-state description of heat exchange leads to a mismatch between irradiance and module efficiency and thus a bias in the modelled power output. In this work a simple four-parameter model is shown to be sufficient to capture the dynamics of PV module temperature as a function of ambient temperature, shortwave and longwave irradiance and wind speed, and the parameters are fitted to measured data using non-linear optimisation.

Several authors have studied the thermal characteristics of PV systems in some detail (see for instance the reviews in Skoplaki and Palyvos, 2009a, b). Popular models currently employed in the field are the King model (King et al., 2004) and the Faiman model (Faiman, 2008); these are simple steady-state models with only a handful of parameters, in which heat exchange is assumed to be instantaneous. Both models give satisfactory results when dealing with coarsely resolved time series, i.e., hourly data, but they perform poorly when applied to high frequency data, precisely because the inherent relaxation time of the system due its heat capacity and total heat exchange with the environment is not taken into account. In particular the temperature response of a PV module lags behind the rapid fluctuations in incoming shortwave irradiance under patchy cloud cover, so that a steady-state temperature model can deviate from reality by up to 25 K. For a modern PV module with 20 % efficiency and a temperature coefficient of 0.4 % K⁻¹ this leads to a relative error of 10 % in the modelled efficiency and resulting power output.

In order to describe the module temperature dynamically one needs to solve the differential equation governing heat exchange between the module and its environment, which has been studied in detail before. Some examples include Fuentes (1987), where an approximate analytical solution is proposed, and Jones and Underwood (2001), who show that the steady-state approach is not appropriate for 1 min time intervals. Other works in this regard are Notton et al. (2005) and Torres Lobera and Valkealahti (2013). In Torres-Lobera and Valkealahti (2014) and Gu et al. (2019) a dynamic thermal model is coupled to an electrical model in order to examine the effect on PV module performance as a whole. In all cases this approach involves iteratively solving a differential equation with several parameters.

In the present work a simple model built on the works of Faiman (2008) and Del Cueto (2000) is modified by applying an exponential smoothing kernel to represent the relaxation time constant, which effectively includes the heat capacity of the system using a matrix that introduces time dependence into the equation. The four model parameters are then extracted from data from two measurement campaigns carried out in autumn 2018 and summer 2019 in the Allgäu region in Germany, as part of the BMWi-funded project MetPVNet. The model was tested and validated on two free-standing systems and one roof-mounted system, respectively.

The model equations are described in detail in Sect. 2. Section 3 outlines the measurements and data collection methods, and the results and conclusions are given in Sects. 4 and  5, respectively.

2 Dynamic temperature model

From physical considerations the module temperature can be described by the heat balance equation

$$\begin{array}{}\text{(1)}& Q_{\mathrm{SW}\mathrm{rad}}-Q_{\mathrm{conv}}-Q_{\mathrm{net}\mathrm{LW}\mathrm{rad}}-Q_{\mathrm{PV}}-Q_{\mathrm{cond}}=\mathrm{0},\end{array}$$

with the terms decreasing in approximate order of importance: the module is heated by shortwave solar radiation and cooled primarily by convection and longwave thermal emission, with the energy losses due to the photovoltaic effect Q_PV (corrected for resistive losses) and conduction Q_cond playing a minor role (see Gu et al., 2019 for an estimation of the importance of each term). Writing this out explicitly leads to a differential equation with the module temperature on both sides (see Eq. A1 in the Appendix), since the cooling due to convection and thermal emission depends on the module temperature itself.

In this work a simplified parametric model is proposed as follows: the module temperature time series T_module is written in matrix notation as

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{\mathit{T}}_{\mathrm{module}}& ={\mathbf{M}}_{\mathit{\tau }}[{\mathit{T}}_{\mathrm{amb}}+{\displaystyle \frac{{\mathit{G}}_{\mathrm{tot},\mathrm{PV}}^{\mathrm{\angle }}}{u_{\mathrm{1}}+u_{\mathrm{2}}{\mathit{v}}_{\mathrm{wind}}}}\\ & +u_{\mathrm{3}}\left({\mathit{T}}_{\mathrm{sky}}-{\mathit{T}}_{\mathrm{amb}}\right)],\end{array}\end{array}$$

where the empirical coeffient u₁ in units of W m⁻² K⁻¹ controls the shortwave heating, u₂ in W s m⁻³ K⁻¹ determines the degree of convective cooling and the dimensionless parameter u₃ controls the effect of longwave thermal emission. The ambient temperature (T_amb), plane-of-array irradiance (${\mathit{G}}_{\mathrm{tot},\mathrm{PV}}^{\mathrm{\angle }}$), wind speed (v_wind) and sky temperature (T_sky) are time series vectors and the matrix M_τ is defined by

$$\begin{array}{}\text{(3)}& {\mathbf{M}}_{\mathit{\tau },ij}=\left\{\begin{array}{ll}\mathrm{0}& \text{for }i-j<\mathrm{0}\\ \frac{\exp \left(-(i-j)\mathrm{\Delta }t/\mathit{\tau }\right)}{C}& \text{for }\mathrm{0}\le i-j\le N\\ \mathrm{0}& \text{for }i-j>N\end{array}\right\},\end{array}$$

where τ is the characteristic time constant, $\mathrm{\Delta }t\equiv t_n-t_{n-\mathrm{1}}$ is the time interval between data points and the normalisation factor is given by

$$\begin{array}{}\text{(4)}& C\equiv \sum _{j=max(\mathrm{0},i-N)}^i\exp \left(-(i-j)\mathrm{\Delta }t/\mathit{\tau }\right).\end{array}$$

In other words, M_τ is a lower triangular matrix with e⁰=1 on the diagonal and the off-diagonal entries along each row are exponential functions decaying with the distance i−j from the diagonal, cut off at $i-j=N-\mathrm{1}$ and normalised by the sum of each row. Multiplying out the matrix terms and assuming for brevity that there are at least N time steps measured before the time point t_n, one gets

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{T}_{\mathrm{module}}\left(t_n\right)& ={\displaystyle \frac{\mathrm{1}}{C^{\prime }}}\sum _{k=\mathrm{0}}^N\exp \left(-k\mathrm{\Delta }t/\mathit{\tau }\right)[T_{\mathrm{amb}}\left(t_{n-k}\right)\\ & +{\displaystyle \frac{G_{\mathrm{tot},\mathrm{PV}}^{\mathrm{\angle }}\left(t_{n-k}\right)}{u_{\mathrm{1}}+u_{\mathrm{2}}{v}_{\mathrm{wind}}\left(t_{n-k}\right)}}+u_{\mathrm{3}}\mathrm{\Delta }{T}_{\mathrm{s},\mathrm{a}}\left(t_{n-k}\right)],\end{array}\end{array}$$

where $\mathrm{\Delta }{T}_{\mathrm{s},\mathrm{a}}\equiv T_{\mathrm{sky}}-T_{\mathrm{amb}}$ and in this case the normalisation constant C^′ is the same for each row of the matrix (in reality the normalisation is only constant after N time steps have passed). This shows that the value of module temperature from each time t_n−k in the past contributes to the current value at time t_n , with an exponentially decreasing weight proportional to kΔt∕τ, up to a time ΔtN. In practice one can simply cut off the exponential function at a small value, which was chosen to be 10⁻⁶ in this work.

Although one would expect the effect of thermal emission to be proportional to $T_{\mathrm{sky}}^{\mathrm{4}}$, by factorising the corresponding term in the differential equation one can show that it is sufficient to approximate the thermal emission by a term linear in the sky temperature (see Appendix A).

The model in Eq. (2) has four unknown parameters: the coefficients u₁, u₂ and u₃ as well as the time constant τ, which depend both on the characteristics of each individual PV system (i.e. its geometry, material properties or the way it is mounted) as well as on the prevailing meteorological conditions of its surroundings. In order to be able to apply the model to any system it is useful to perform a parameter estimation procedure using experimental data. This so-called “forward model calibration” is performed using non-linear inversion (Rodgers, 2000) with the Levenberg-Marquardt method. The parameter values that give the best fit between the model and the data can then be used to model the module temperature at an arbitrary time point.

3 Field measurements

3.1 Photovoltaic systems

The model was validated using data from two different stations and three different PV systems. The first station is a large free-standing solar park made up of 504 modules of 180 Wp each. The solar park is just outside Kempten, Allgäu, close to the Iller river, and a pyranometer measuring station (see Fig. 1) as well as an anemometer on a 3 m mast were erected on site. PV module temperature (at the back of two PV modules) was recorded in 15 s intervals, wind speed in 20 s intervals and irradiance and ambient temperature (measured at the pyranometer station) in 1 s intervals.

Figure 1 PV system and measurement station with horizonal and plane-of-array pyranometer along with a small weather station measuring ambient temperature at station 1, situated at 47.683233^∘ N, 10.319028^∘ E.

At the second station on a farm east of Kempten, two different PV systems were used to validate the model. System 2A is a small system (roughly 6 kWp) with a steep elevation angle of roughly 60^∘ and is well ventilated from behind as can be seen in Fig. 2, whereas System 2B is a larger roof-mounted system on top of a barn (see Fig. 3). In both cases a temperature sensor was mounted behind the PV modules. A pyranometer station identical to that in Fig. 1 measured irradiance in the plane of the array of system 2A, whereas for system 2B a Kipp & Zonen RT1 sensor was used for this purpose, and an anemometer on a 5 m mast was erected closeby.

Figure 2 PV system 2A at station 2 (47.653161^∘ N, 10.496584^∘ E), where the smaller system that reaches from the roof to the ground was used for temperature modelling.

Figure 3 PV system 2B at station 2, with a Kipp & Zonen RT1 sensor mounted on the edge of the module in order to measure plane-of-array irradiance and module temperature.

Table 1 Data frequency, measurement uncertainty and measurement time periods for the three PV systems.

Table 1 summarises the different quantities measured during the two measurement campaigns, with their respective frequencies and uncertainties. For the temperature modelling all data was downsampled to a period of 1 min using a moving average function.

3.2 Longwave atmospheric emission

The longwave downward welling irradiance was measured with a frequency of 2 Hz and an uncertainty of 2 % using a secondary standard Kipp & Zonen pyrgeometer, situated on the roof of a high-rise building in Kempten. Although this device is not exactly co-located with the PV systems it still gives a general idea of the sky temperature and improves the model fit, especially in the early morning and late evening. The sky temperature is simply calculated from the irradiance measurements using

$$\begin{array}{}\text{(6)}& {\mathit{T}}_{\mathrm{sky}}=\sqrt[\mathrm{4}]{{\displaystyle \frac{{\mathit{G}}_{\mathrm{LW}}^{\downarrow }}{\mathit{ϵ}\mathit{\sigma }}}},\end{array}$$

with an emissivity of ϵ=1 and σ the Stefan-Boltzmann constant. Any deviations from blackbody emissions as well as a reduction in the field of view due to the tilt of the PV modules will be captured in the variation of the coefficient u₃ in Eq. (2).

4 Results

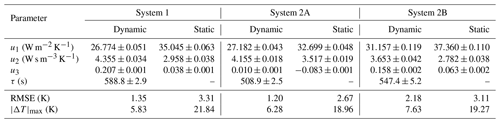
The model in Eq. (2) (referred to as the “dynamic” model) was fitted to the module temperature for the three systems described above, for different days during the measurement campaigns in 2018 and 2019. To illustrate the effect of adding time-dependence to the model, another fit with the so-called “static” or time-independent model was performed, with the parameters $u_{\mathrm{1},\mathrm{2},\mathrm{3}}$ allowed to vary but with τ=0. The number of days of each type are shown in Table 2, as well as the time of year in which the measurements were taken. The multiparameter fit was performed for all days at once: the third column of Table 2 gives the total number of data points for each system, i.e., the length of the time series vectors in Eq. (2) in 1 min resolution. Note that only data up to a solar zenith angle (SZA) of 95^∘ were considered.

Table 2 Number of days of each type and total number of data points used for the parameter retrieval for each system.

Table 3 Results for all-sky conditions for both the static and dynamic models.

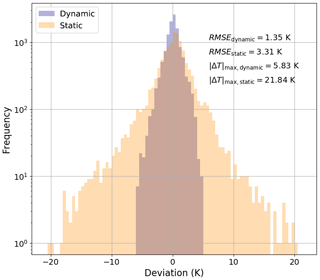
Figure 4 Histogram of the deviation between modelled and measured module temperature at system 1, for both the dynamic and static models and under all-sky conditions (i.e., all available days).

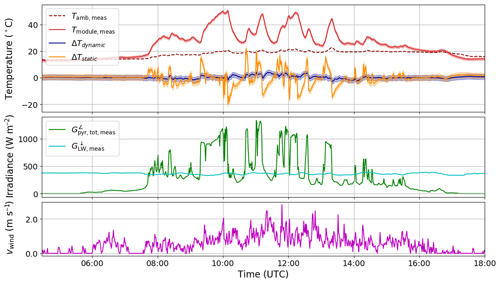
Figure 5 Comparison of dynamic and static temperature modelling for system 1 on 14 September 2018. Measured module temperature (red) is plotted together with the deviation between modelled and measured module temperature for the dynamic (blue) and static (orange) models, along with ambient temperature (dark red dashed), in units of ^∘C. Shortwave (green) and longwave (cyan) irradiance as well as wind speed (magenta) are also shown.

The a priori values of the unknown parameters were taken to be

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& u_{\mathrm{1},\mathrm{a}}=\mathrm{25}\mathrm{W}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{K}}^{-\mathrm{1}},u_{\mathrm{2},\mathrm{a}}=\mathrm{7}\mathrm{W}\mathrm{s}{\mathrm{m}}^{-\mathrm{3}}{\mathrm{K}}^{-\mathrm{1}},\\ & u_{\mathrm{3},\mathrm{a}}=\mathrm{0.25},\mathrm{and}{\mathit{\tau }}_{\mathrm{a}}=\mathrm{600}\mathrm{s},\end{array}\end{array}$$

with an a priori uncertainty of 20 % for the parameters u_i,a ($i=\mathrm{1},\mathrm{2},\mathrm{3}$) and 50 % for τ_a. The results of both modelling approaches are compared in Table 3, for all-sky conditions (i.e., all available days). It is evident that the dynamic model shows a better fit to the data: the RMSE is roughly halved from 3.03 to 1.58 K, on average. An even larger reduction can be seen in the maximum absolute deviation $|\mathrm{\Delta }T{|}_{\max }$: the static model has a maximum absolute deviation ranging from 18.96 to 21.84 K, with a mean of 20.02 K, whereas the dynamic model gives a range of 5.83 K $\le |\mathrm{\Delta }T{|}_{\max }\le \mathrm{7.63}$ K and a mean of 6.58 K. The histogram in Fig. 4 shows that the error in the static model for system 1 has a much larger spread than that of the dynamic model. This shows that in order to correctly model the instantaneous temperature of PV modules one has to consider a dynamic approach.

Figure 5 shows the model results for system 1 on 14 September 2018, a day with high variability in global radiation. The measured temperature with its uncertainty can be compared to the modelled temperature using both models, and the corresponding ambient temperature, irradiance and wind speed are plotted for completeness. The dynamic model can reproduce the measured module temperature, even during times with fluctuating irradiance. The time constant is found to be of the order of 10 min (see Table 3), which can also be seen by examining the typical width of the troughs and peaks in the temperature curve during cloudy conditions. In addition, after sunset the module temperature falls below ambient temperature and the inclusion of longwave thermal emission in the model allows the temperature at this time of day to be modelled accurately.

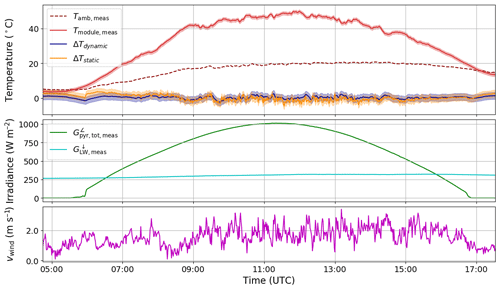
Figure 6 Comparison of dynamic and static temperature modelling for system 2A on 27 September 2018, see the caption of Fig. 5 for details.

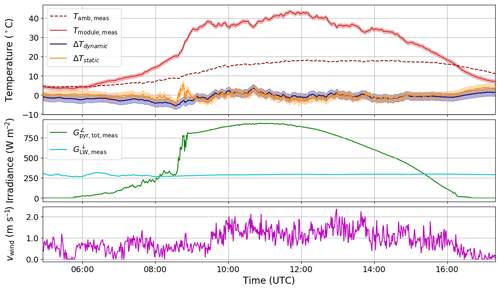
Figure 7 Comparison of dynamic and static temperature modelling for system 1 on 4 October 2018, see the caption of Fig. 5 for details.

The model can also reproduce the thermal behaviour on a clear sky day, as shown in Fig. 6. In this case the static model reproduces the high frequency variations in temperature due to the varying wind speed, whereas the dynamic model smooths them out (the exponential term acts like a lowpass filter). Note that the non-linear fitting procedure was applied to all data at once (both clear and cloudy days), so that the algorithm finds the optimal parameters that will minimise the cost function over the entire time series (see Table 2). One case in which the model shows a larger deviation from measurement is in the presence of low-lying fog, as can be seen in Fig. 7, for system 1 on 4 October 2018. A cloud camera next to the system confirmed the presence of fog, and since the module temperature is higher than predicted it is most probably due to an incorrect sky temperature, since the measurement of thermal emission is situated north of the PV system on a high-rise building with different overhead conditions.

5 Conclusions

In this work a simple four-parameter dynamic thermal model for the temperature of PV systems was proposed, and the model was fitted to data from three different systems using non-linear optimisation. By employing an exponential smoothing kernel it was shown that the time constant (and therefore the heat capacity) of the system can be extracted from data, and the dynamic model could reproduce 1 min instantaneous temperature measurements with an RMSE of between 1.20 and 2.18 K and a maximum absolute deviation of between 5.83 and 7.63 K. Further improvements to this work could be achieved by considering reflection losses as well as losses due to power generation. It could also be conceivable to use the measured PV power to estimate the sky temperature, so that a longwave irradiance measurement is not needed. A comprehensive comparison of the differential equation approach with the method presented here will be carried out in future work.

Appendix A: Physically motivated approach

From the heat balance equation in Eq. (1) and ignoring conduction one can write down the differential equation for the thermal exchange between a free-standing PV module with inclination angle θ and its environment as

$$\begin{array}{}\text{(A1)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{C_{\mathrm{module}}}{A}}& {\displaystyle \frac{\mathrm{d}{T}_{\mathrm{module}}}{\mathrm{d}t}}={\mathit{\alpha }}_{\mathrm{PV}}^{\downarrow }{G}_{\mathrm{tot},\mathrm{PV}}^{\mathrm{\angle }}-h_{\mathrm{conv}}\\ & \left(T_{\mathrm{module}}-T_{\mathrm{amb}}\right)\\ & -\mathit{\sigma }\left[{\mathit{ϵ}}_{\mathrm{glass}}{\displaystyle \frac{\mathrm{1}+\cos \mathit{\theta }}{\mathrm{2}}}+{\mathit{ϵ}}_{\mathrm{tedlar}}{\displaystyle \frac{\mathrm{1}-\cos \mathit{\theta }}{\mathrm{2}}}\right]\\ & \left(T_{\mathrm{module}}^{\mathrm{4}}-T_{\mathrm{sky}}^{\mathrm{4}}\right)\\ & -\mathit{\sigma }\left[{\mathit{ϵ}}_{\mathrm{glass}}{\displaystyle \frac{\mathrm{1}-\cos \mathit{\theta }}{\mathrm{2}}}+{\mathit{ϵ}}_{\mathrm{tedlar}}{\displaystyle \frac{\mathrm{1}+\cos \mathit{\theta }}{\mathrm{2}}}\right]\\ & \left(T_{\mathrm{module}}^{\mathrm{4}}-T_{\mathrm{ground}}^{\mathrm{4}}\right)-{\mathit{\eta }}_{\mathrm{module}}{G}_{\mathrm{tot},\mathrm{PV}}^{\mathrm{\angle }},\end{array}\end{array}$$

where η_module is the electrical efficiency, C_module is the heat capacity in J K⁻¹, h_conv is the convective coefficient in W K⁻¹ m⁻², ${\mathit{\alpha }}_{\mathrm{PV}}^{\downarrow }$ is the absorptivity for shortwave radiation at normal incidence, ϵ_glass (ϵ_tedlar) is the emissivity for longwave radiation from the glass (tedlar) surface and σ is the Stefan-Boltzmann constant.

Assuming that ${\mathit{ϵ}}_{\mathrm{glass}}={\mathit{ϵ}}_{\mathrm{tedlar}}\equiv \mathit{ϵ}$, the thermal emission term in Eq. (A1) can be rewritten as

$$\begin{array}{}\text{(A2)}& {\displaystyle }\begin{array}{rl}\mathit{ϵ}\mathit{\sigma }(T_{\mathrm{module}}^{\mathrm{4}}-T_{\mathrm{sky}}^{\mathrm{4}})& =[\mathit{ϵ}\mathit{\sigma }\left(T_{\mathrm{module}}^{\mathrm{2}}+T_{\mathrm{sky}}^{\mathrm{2}}\right)\\ & \left(T_{\mathrm{module}}+T_{\mathrm{sky}}\right)]\left(T_{\mathrm{module}}-T_{\mathrm{sky}}\right)\\ & \equiv h_{\mathrm{rad},\mathrm{s}}\left(T_{\mathrm{module}}-T_{\mathrm{sky}}\right),\end{array}\end{array}$$

and it turns out that the term h_rad,s is roughly constant. A similar term h_rad,g can be written for the term dependent on T_ground, for which the same conclusion applies. This approach is used in Fuentes (1987) in order to calculate an approximate analytical solution to Eq. (A1), and in this way the simple parametric models can be shown to be approximately equivalent to the physically motivated approach. A comprehensive comparison will be carried out in future work.