Observation of wave-driven air–water turbulent momentum exchange in a large but fetch-limited shallow lake

Wind-induced waves play a key role in air–sea momentum and heat exchange. Fetch-limited shallow lakes differ significantly from open ocean circumstances since the wave field is characterized by young and growing waves that (i) are steeper and can collapse by white-capping at lower wind speeds, and (ii) travel with lower phase velocity. Consequently, momentum (and heat) flux estimation methods arising from oceanographic observations cannot be directly applied; however, few attempts have been made to describe air–water turbulent exchange in case of large, but still fetch-limited shallow lakes. Within a Croatian-Hungarian measurement campaign, turbulent flux measurements were performed in Lake Balaton. Momentum and heat fluxes were measured with eddy-covariance technique at an offshore station, while waves were simultaneously recorded with underwater acoustic surface tracking. Momentum fluxes were also recorded at two further stations closer to the shore. In this study, we analyze the measured wind stress and surface waves to reveal surface drag in case of highly fetch-limited conditions. We compare our results with relevant model formulations that attempt to estimate momentum flux using different wave state parameterizations (i.e. wave age and wave slope modified Charnock formulations) and show that derived drag and roughness length parameterizations differ significantly from oceanographic formulas.

1 Introduction

The wind driven momentum exchange at the air-water interface is a key driver of hydrodynamic and ecological processes in freshwater lakes. It generates currents, surface waves and turbulent mixing that directly affects sediment transport (Olabarrieta et al., 2012), stratification characteristics (Torma and Krámer, 2017a) and oxygen conditions (Istvánovics and Honti, 2018). Moreover, it is a complex process due to different interactions which occurs between the atmosphere and the water. One of the fundamental interactions is created by surface waves which provide feedback on momentum flux by determining the drag of the water surface.

There are two common methods to determine momentum flux at the air–water interface. The wind friction velocity (u_*) can be calculated by: (i) drag coefficient based on bulk formulas as a function of wind speed, or by (ii) estimating a (stability corrected) logarithmic wind velocity profile over the water surface. Bulk formulas are simple to use; however, drag coefficient (C_D) values are varying over a wide range, between 0.0005–0.004 (see figures below for references). Furthermore, Taylor and Yelland (2001) experienced that existing formulas, developed based on various oceanographic datasets, cannot predict the observed higher surface drag in Lake Ontario due to very young wave states. In case of the wind profile estimation method, both the momentum flux (or u_*) and the roughness length (z₀) of the wavy surface are unknown. The best-known and most commonly used roughness length calculation method is the Charnock-relation. In this relation, z₀ linearly depends on the Charnock-coefficient (α), which has an average value of 0.012–0.018 in the literature. Vickers and Mahrt (1997) stratified measurements by fetch and they measured α=0.018 for onshore and α=0.073 for offshore wind conditions during the RASEX campaign. To our knowledge, they observed the highest α value so far.

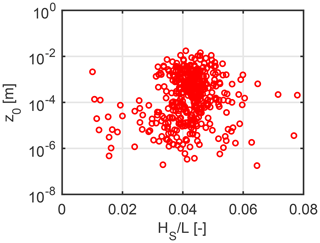
Drag coefficients and roughness lengths are often related to wave conditions. On the one hand, wave state can be characterized by the wave age ($c_{\mathrm{p}}/u_{*}$) or inverse wave age ($u_{*}/c_{\mathrm{p}}$), where c_p is the wave phase speed. Latter one varies between $u_{*}/c_{\mathrm{p}}=\mathrm{0.02}$–0.2 in the oceanographic literature, in contrast, according to our observations with short (∼3 km) fetch, inverse wave age varies between $u_{*}/c_{\mathrm{p}}=\mathrm{0.1}$–0.5. To show the importance of wave age type parameterizations, one can mention Lin et al. (2002) who found that drag coefficients correlate better with wave age than with wind speed. Many studies prefer to combine wave state parameterization with the Charnock-formula by establishing wave dependent α-equations; however, it is more advantageous to relate wave age directly to the roughness length (or to its normalized value) in order to avoid self-correlation by double-counting u_* (Johnson et al., 1998; Smith et al., 1992; Drennan et al., 2003; Fisher et al., 2015). Finally, wave state can be also characterized by wave steepness (H_s∕L), where H_s is the significant wave height and L is the wave length. Wave steepness varies between $H_{\mathrm{s}}/L=\mathrm{0.02}$–0.06 both in the literature and in our measurements.

The motivation of this study is to determine momentum flux for a large, but strongly fetch-limited lake, partly for hydrodynamic modelling purposes. Several studies applied coupled numerical ocean-atmosphere-wave models (Rizza et al., 2018; Shi et al., 2019) using available momentum flux formulations for oceanographic environment to explore the effect of interaction processes. The main feature that generates deviation from oceanographic conditions is the short fetch. As a result, the wave field is characterized by very young and high frequency waves and measured inverse wave age values are far above the literature data. Consequently, the available estimation formulations from the oceanographic literature are not applicable to estimate the momentum exchange in highly fetch-limited conditions in general. Our hypothesis is that the resistance of the airflow over young and steep waves is higher than in typical open or even coastal oceanographic environments. In this study, we focus only on the momentum flux by means of datasets gained from two simultaneously operating eddy-covariance stations in Lake Balaton.

2 Study site and instrumentation

In order to prove our hypothesis, we collected high quality turbulent flux data at several locations in Lake Balaton (Hungary). The FIMO-CROHUN (FIrst MicrometeOrological research within the CROatian-HUNgarian collaboration) measurement campaign lasted one month from 31 August until 10 October 2018. Lake Balaton is a shallow, but large lake with a mean depth of 3.3 m, surface area of 596 km², length of 78 km and mean width of 7.5 km. The fetch varies between 2–10 km in case of prevailing wind directions. To gain a detailed insight into spatial variation of momentum exchange, we set up three measurement stations in the westernmost basin along the fetch of the prevailing NNW wind direction. Station B was located in the middle of the basin, while station A and C were near the NW and S shorelines, respectively (Fig. 1).

Figure 1 Study site: bathymetry map and station locations. Photos of measurement station B and C.

At the offshore station (B), turbulent fluxes were measured by an eddy-covariance set-up placed at 6.2 m height above the water surface, which consisted of a Campbell CSAT3 sonic anemometer and a Campbell EC150 open path CO₂∕H₂O gas analyser, operating at 10 Hz. At the southern onshore station (C), two Gill Windmaster sonic anemometers were placed at 3.0 and 7.0 m height, both operating at 10 Hz. Flux measurements were complemented with routine weather observations, such as air temperature and relative humidity. Water surface temperature was measured by Campbell T107 sensor 2 cm below the surface by means of a floating plate.

At station B, wave conditions were measured as well by an upward looking Nortek Signature1000, which was mounted over the lakebed. The instrument was operating in burst mode and collected 4096 samples at 4 Hz at every 20 min.

3 Methodology

High-frequency, raw EC time-series were post-processed by the TK3 software (developed at Bayreuth University) to derive momentum fluxes (Mauder and Foken, 2011). Post-processing consisted of spike removal (with no filling up of missing values) and several correction steps, such as double rotation method to correct anemometer tilt (McMillen, 1988; Wilczak et al., 2001); Moore correction to reduce spectral loss; Schotanus correction for buoyancy flux (Foken et al., 2004); Webb-correction for density fluctuation effects (Webb et al., 1980). Turbulent fluxes were evaluated as 20 min averages.

The quality of turbulence measurements was assured by the evaluation system of Foken et al. (2004) which distinguishes 9 quality classes (QC) using multiple tests. Low-quality data have been filtered with quality assurance (QA) thresholds based on literature and detailed sensitivity analysis. A flux data was accepted if QC < 7 and the flux variance test showed less than 40 % difference between measured and theoretical values. Minimum limiters have been also applied as filters to ensure stationarity, like ΔU_10N<50 % and Δdir < 30 ^∘, where Δ means the difference between two consecutive 20 min average values. Two limiters have been applied for very low winds, like U_10N>2 m s⁻¹ and $u_{*}>\mathrm{5}$ cm s⁻¹ to exclude underdeveloped turbulence and buoyancy force dominated free convection (Abdella and D'Alessio, 2005).

Raw acoustic surface tracking data of Signature1000 were post-processed to derive actual wave conditions. Post-processing included detrending and spike filtering with linear interpolation, and resulted in bulk wave parameters for each burst by means of spectral analysis following Holthujsen (2007). Zero-crossing method was also used as a control. Besides significant wave height, peak period and wave length further wave state parameters were calculated, like wave age which is the ratio of the friction velocity and the wave phase speed ($u_{*}/c_{\mathrm{p}}$) and wave steepness, which is the ratio of the significant wave height and the wavelength (H_s∕L). For station C, wave heights and periods were estimated using the US Army Corps' Shore Protection Manual equations from wind speed, water depth and fetch data. The estimation method was validated beforehand against wave measurements from station B. Wave data have been quality controlled as well, which consisted of a restriction to fetch-limited conditions by filtering out duration-limited conditions and also a minimum limiter of H_s>5 cm has been applied.

In the first part of the paper, drag coefficient and roughness length formulations were derived by the following procedure: first, universal stability functions were selected following Dyer (1974). Second, roughness lengths were calculated by rearranging the stability corrected logarithmic velocity profile (Eq. 1):

$$\begin{array}{}\text{(1)}& U_z={\displaystyle \frac{u_{*}}{\mathit{\kappa }}}\left(\ln \left({\displaystyle \frac{z}{z_{\mathrm{0}}}}\right)-{\mathit{\psi }}_m\left({\displaystyle \frac{z}{L}}\right)\right),\end{array}$$

where U_z is the wind speed at the z measurement level, u_* is the friction velocity, z₀ is the roughness length, κ is the Karman-constant, and ${\mathit{\psi }}_m\left(\frac{z}{L}\right)$ is the stability function in which L is the Obukhov-length. In the third step, measured wind speed was corrected to 10 m height and to neutral stability in the knowledge of roughness length and EC derived friction velocity, using (Eq. 2):

$$\begin{array}{}\text{(2)}& U_{\mathrm{10}\mathrm{N}}={\displaystyle \frac{u^{*}}{\mathit{\kappa }}}\cdot \ln \left({\displaystyle \frac{\mathrm{10}}{z_{\mathrm{0}}}}\right),\end{array}$$

where U_10N is the 10 m neutral wind speed. Finally, neutral 10 m drag coefficient and Charnock-parameter values were calculated, by means of following equations (Eqs. 3 and 4), respectively:

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }{u}_{*}^{\mathrm{2}}=C_{\mathrm{D}\mathrm{10}\mathrm{N}}\cdot U_{\mathrm{10}\mathrm{N}}^{\mathrm{2}},\text{(4)}& {\displaystyle }& {\displaystyle }{z}_{\mathrm{0}}=\mathit{\alpha }\cdot {\displaystyle \frac{u_{*}^{\mathrm{2}}}{g}}+\mathrm{0.11}\cdot {\displaystyle \frac{\mathit{\nu }}{u_{*}}},\end{array}$$

where C_D10N is the 10 m neutral drag coefficient, α is the Charnock-coefficient, g is the gravitational acceleration, and ν the kinematic viscosity of air, respectively. Drag coefficient, Charnock-constant and roughness length relations were set up by curve fittings as a function of wind speed and wave state parameters. In the second part, momentum flux estimations have been performed by the iterative Monin–Obukhov Similarity Theory (MOST), using the same atmospheric stability functions and the obtained roughness length formulations. Model estimations have been analysed, compared and validated against EC fluxes.

4 Results and discussion

4.1 Drag coefficient

Following the literature, we aimed to determine a drag coefficient relation as a linear function of wind speed. Due to the sophisticated quality control, 75 % of the data was rejected, of which 90 % are below 4 m s⁻¹, when turbulence can be dominated by buoyancy-effects (Fig. 2). In the remaining 10 %, stationarity conditions were not fulfilled. In the end, after applying the different QA filters, a straight line was fitted to 465 points. The minimum wind speed was determined as 2 m s⁻¹ by a QA filter, while the maximum observed wind speed reached 18 m s⁻¹. The obtained drag coefficient equation is $C_{\mathrm{D}\mathrm{10}\mathrm{N}}=(\mathrm{0.88}+\mathrm{0.099}\cdot U_{\mathrm{10}\mathrm{N}})\cdot {\mathrm{10}}^{-\mathrm{3}}$.

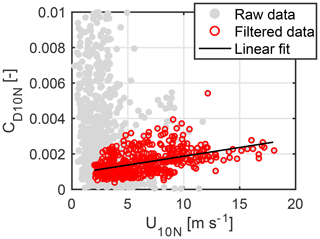
Figure 2 Raw and filtered (quality controlled) scatter data of drag coefficients (C_D10N) as a function of neutral 10 m height wind speed (U_10N).

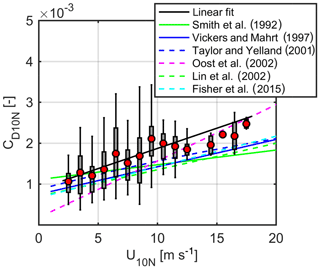
In Fig. 3, we present the observations in a bin-averaged manner with whiskers, showing means with red filled circles, 25th and 75th percentiles with boxes and ±2.7σ values with lines using a bin-size of 1 m s⁻¹. Between the 8–9 and 9–10 m s⁻¹ bins there is a stepwise increase in the drag coefficient. By comparing the obtained relationships with well-known functions from the literature, one can assess that these functions would clearly underestimate the drag for our highly fetch-limited conditions. In the literature equations, the average offset is $\mathrm{0.68}\times {\mathrm{10}}^{-\mathrm{3}}$ and the average multiplier is $\mathrm{0.077}\times {\mathrm{10}}^{-\mathrm{3}}$ (see list of references in Fig. 3) that are ∼30 % lower than our fitted parameters. We highlight the equation of Vickers and Mahrt (1997) since they have observations with similar fetch (2–5 km). The slope of their equation is close to ours; however, their drag coefficients are significantly lower in the whole wind speed range. The linear equation from Oost et al. (2002) would estimate the momentum flux for winds above 8–9 m s⁻¹ well, but it is too steep, and it would not be accurate for lower winds. Although, Oost et al.'s (2002) observations are characterized by ∼9 km fetch, which is about three-times higher than in Lake Balaton. Other parameterizations shown in the figure would underestimate the drag especially for higher wind speeds (Smith et al., 1992; Taylor and Yelland, 2001; Lin et al., 2002; Fisher et al., 2015).

Figure 3 Drag coefficient as a function of neutral 10 m height wind speed.

The observed significant scatter suggests that other parameters should be involved in order to truthfully model momentum exchange at the wavy air–water interface. A great number of studies reported wave-age based drag coefficient formulations. Our drag coefficient-wave age relation, $C_{\mathrm{D}\mathrm{10}\mathrm{N}}=\mathrm{0.0037}\cdot (\frac{c_{\mathrm{p}}}{u_{*}}{)}^{-\mathrm{0.5}}$ differs more remarkably from published functions (Fig. 4), which would overestimate momentum flux over Lake Balaton. The referred relationships (see Figs. 4 and 5 for references) have been arising from oceanography where wave conditions are characterized by more mature waves (typically $c_{\mathrm{p}}/u_{*}>\mathrm{15}$) and these (fitted) curves become steep in the range of very young waves. The obtained wave age based formulation is contradictory with the cited wind speed related results; however, it strengthens the need that new functions have to be formulated in case of strong fetch limitation and very young wave states.

Figure 4 Drag coefficient as a function of wave age.

Figure 5 Charnock-coefficient (α) as a function of wave age.

4.2 Roughness length

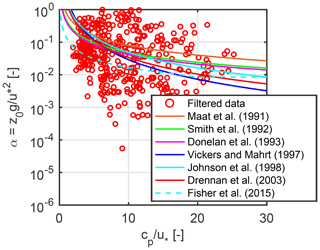
A physically well-founded method of momentum exchange calculation is the Monin–Obukhov similarity theory that assumes a constant stress layer and stability dependent logarithmic velocity profile above the surface. The surface is characterized by the roughness length, which is dynamically changing in case of a wavy water surface. The most commonly used Charnock-relation determines the roughness length of water surface as a function of friction velocity and the Charnock-coefficient. In the simplest case this α parameter is a constant. Using u_* (provided by EC) and applying the MOST, we derived α for each 20 min averages. The mean of the measured α values is 0.035. This average α is about three-times higher than the literature average of 0.012–0.018 or the upper limit of 0.028 determined by Edson et al. (2013) however, it is below 0.073 published by Vickers and Mahrt (1997). Yet, this result confirms our hypothesis about the higher surface drag in case of fetch-limited conditions.

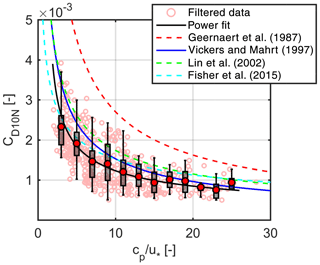
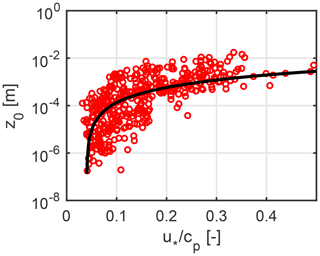
We attempted to set up a traditional Charnock-type relation that incorporates the effect of waves, as many similar formulations have been found in the literature. Nevertheless, a very weak relationship was found between the Charnock-coefficient and the wave age (Fig. 5) or wave steepness. To avoid the self-correlation in the Charnock-relation, it is advantageous to correlate observed roughness lengths directly with wave parameters (Johnson et al., 1998; Drennan et al., 2003). On the one hand a very weak correlation was found between the roughness length and wave steepness (Fig. 6), while on the other, a more reliable relationship is observed with the inverse wave age (Fig. 7). The point cloud, while still quite scattered, shows an asymptotical behaviour towards increasing $u_{*}/c_{\mathrm{p}}$ with maximal roughness of 5 mm on which a power-type equation was fitted. So, in case of young wave states, the younger the wave, the greater the roughness length.

Figure 6 Roughness length as a function of wave steepness.

Figure 7 Roughness length as a function of inverse wave age.

4.3 Momentum flux estimation

In order to evaluate the derived Charnock-coefficient (α=0.035) and wave age related z₀ parameterization, the momentum flux was estimated using the profile method. The wind velocity profile was determined by iteration in the constant stress layer according to the MOST. The estimated and measured friction velocity values are compared in Fig. 8. Surprisingly, both models are equally good and have high coefficient of determinations (R²=0.91). Despite of its simplicity, the Charnock-relation does not underperform the wave age based parametrization. This suggest that the obtained α characterize offshore drag conditions well for ∼3–4 km of fetch. Nevertheless, its lake wide applicability is still questionable in the absence of spatial momentum flux data.

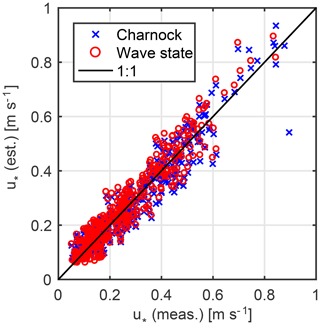
Figure 8 Estimated and measured momentum fluxes (friction velocities) using constant Charnock-coefficient (blue crosses) and wave age based roughness length parameterization (red circles).

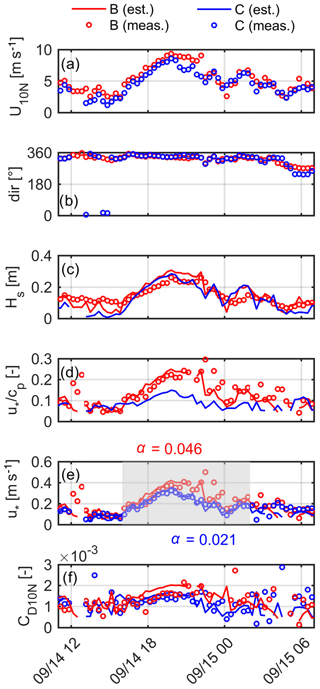
Figure 9 Time series of (a) wind speed, (b) wind direction, (c) significant wave height, (d) wave age, (e) friction velocity and (f) drag coefficient for the selected wind event. Red colour represents station B, while blue colour represents station C. Observations are plotted with circles, model calculations with continuous lines.

4.4 Spatial variability

The presented considerably good estimation of momentum flux using a constant Charnock-coefficient for station B can be attributed to the fact that the station is located in the middle of the basin having the same ∼3–4 km of fetch in case of any wind directions. By extending the analysis to several locations, the use of the Charnock-constant might be reconsidered. To explore the spatial variability of wind field and momentum exchange, a 20 h-long wind event was analysed based on simultaneous friction velocity measurements at stations B and C. The event was a moderate storm blowing constantly from the prevailing NNW direction with a 10 m s⁻¹ maximum wind speed. Figure 9a and b show measured time series of wind speed and wind direction at each stations. The wind speed is increasing from ∼2 to ∼10 m s⁻¹ between 15:00 and 20:00 LT on 4 September 2018. The peak intensity is followed by a slower decrease. In this situation, both stations represent offshore conditions, since station C is on the leeward shore. As a result of internal boundary layer development, we expected that the wind speed will be higher at station C where the fetch was ∼6 km compared to B where it was only ∼3.5 km (Torma and Krámer, 2017b). But instead of that the wind speed was slightly smaller at longer fetch, suggesting that some other mesoscale process might dominate the wind field above the lake. Wave parameters have been estimated for both stations from locally measured wind speed, fetch and water depth. In case of station B, wave estimation has been performed only to validate and prove the reliability of the wave model (Fig. 9c). On the one hand, significant wave heights are quite similar at the two locations, considering both time evolutions and magnitudes. The maximum wave height in both location is almost 30 cm. On the other hand, inverse wave age is remarkably lower at station C, especially at higher wind speeds >7 m s⁻¹, due to the longer fetch. Although wave heights are nearly the same, the change in wave lengths due to the longer fetch doubles the wave age in the vicinity of station C. The maximum inverse wave age values are 0.25 and 0.14 at location B and C, respectively. In of Fig. 9e, measured momentum flux values are plotted with circles, from which Charnock-coefficients were derived for the shaded time period for both stations. At the beginning of the storm, friction velocities were nearly the same, while starting from the evolution period friction velocity was continuously higher at location B which possess shorter fetch. The average α is equal to 0.021 and 0.046 for station C and B, respectively. This is well aligned with the obtained wave age – roughness length relation, namely, the surface roughness decreases with increasing wave age in case of very young waves ($c_{\mathrm{p}}/u_{*}<\mathrm{15}$). Finally, in Fig. 9f, derived drag coefficients are shown, from which it can be concluded that younger waves produce stronger drag. So, the spatial variability is significant, and the momentum flux cannot be estimated using a constant α for the whole basin. However, the spatial variation of the wave field can be accurately estimated using local wind measurements. Consequently, the wave age relation based roughness length estimation can capture to some level the spatial variation of momentum exchange at the air–water interface. Applying the earlier derived roughness length equation, estimated momentum fluxes agree well with measured values on both stations. In terms of drag coefficients, we observe smaller deviation, nevertheless, the drag is continuously smaller at the station with higher fetch and greater wave age.

5 Conclusions

Our hypothesis that the surface drag is remarkably higher in very young wave states compared to open ocean conditions has been confirmed by means of eddy-covariance and acoustic surface tracking wave observations. The very young wave state is the consequence of the fetch limitation that is a typical feature of mid- and large-size freshwater lakes, like Lake Balaton. The two momentum flux estimation methods, namely the drag coefficient based bulk function and the MOST based profile estimation, are both robust after fitting their parameters to fetch limited conditions. The new parameters have been derived based on one-month-long observations, from which reliable datasets have been gained thanks to a rigorous quality control. We note that this study did not deal with momentum fluxes during low winds that represented 75 % of the data. To our knowledge, this type of research was only performed in oceanographic circumstances.

The MOST based wind profile calculation method is physically more founded, albeit it requires stability functions and a roughness length model which describes the drag of the wavy water surface. Based on eddy-covariance observations, we have reassessed the Charnock-coefficient in fetch-limited conditions that resulted in an average value of 0.035, which is remarkably higher than what is commonly found in the literature. We established a roughness length–inverse wave age relationship, which avoids self-correlation in terms of friction velocity. Both roughness length formulations perform equally well for a local momentum flux estimation. The involvement of a second, simultaneously operating EC station into the analysis revealed that spatial variation is remarkable even for very young wave age conditions. In contrast to the original Charnock-formula, the wave age based relationship considers the wave induced spatial variability of wind shear stress and can be directly applied in hydrodynamic lake models to simulate wind induced waves and currents.

Several studies revealed the importance of the air–sea interaction by means of coupled ocean-atmosphere-wave modelling and analysed the effect of wind–wave interactions from different aspects (e.g. Olabarrieta et al., 2012; Shi et al., 2019). The former group obtained better agreement between the measured and simulated wave growth and surface currents by incorporating the wave age dependent roughness parameterization. These works were performed in oceanic conditions and cannot be directly applied at lake scales. However, by the obtained relationships we can aim to explore the effect of the wind-wave interaction driven spatially varying momentum flux on lake hydrodynamics.